ステップカット [DISCO presents ﾃﾞｨｽｶﾊﾞﾘｰﾁｬﾝﾈﾙ ｺｰﾄﾞｺﾝﾃｽﾄ2016 予選 B]

atcoder.jp

問題文の理解にずいぶん時間がかかってしまいました。ではその問題文を整理してみたいと思います。

①半径Rの円を縦にN等分することを考える。

②その際、N-1本の切断線ができるはずである。これをカットラインと呼ぶ。
　・カットラインに、上から1,2,3......N-1の番号を付ける。
　・ただし便宜上、0以下・N以上のカットラインも存在することとする。

③切断するための機械には刃が2枚あり、i番とi-M番のカットラインを同時に切断することができる。
　・カットラインを完全に切断するためには、刃を2回通過させる必要がある。
　・2本のカットラインを同時に切断するとき、カット長（機械の稼働距離）は長い方のカットラインが基準になる

④[1番&1-M番]のカットラインの切断から開始し、[2番&2-M番],[3番&3-M番],[4番&4-M番]……[N-1+M番&N-1番]のカットラインまで動作させる。これにより、全てのカットラインに刃を2回通すことができる。以上のように動作させたとき、カット長の総和はどれだけになるか。

いやあ、複雑ですね。問題文の状況を具体的に頭の中にイメージする能力が必要みたいです。

以下が私の書いたコードになります。

//ddcc2016qual-b

import java.math.BigDecimal;
import java.util.*;

class Main {
	static Scanner sc = new Scanner(System.in);
	static double r;
	static int n;
	public static void main(String[] args) {
		
		r = sc.nextDouble();
		n = sc.nextInt();
		int m = sc.nextInt();
		
		double sum = 0;
		for (int i=1; i<=n-1+m; i++) {
			sum += Math.max(calc(i), calc(i-m));
		}
		System.out.println(BigDecimal.valueOf(sum));
		
	}
	
	//x番目のカットラインの長さはどれだけか？
	static double calc (int x) {
		
		//カットラインが円の外の場合は0
		if (x<=0 || n<=x) return 0;
		
		//x番目のカットラインから円の中心までの距離d
		double d;
		if (n%2 == 0) {
			if (x > (n+1.0)/2) x = n-x;
		}
		else {
			if (x > n/2+1) x = n-x;
		}
		d = r - (2*r/n)*x;
		
		return 2*Math.sqrt(r*r-d*d);
	}
	
}

forループでは「i番とi-m番のカットラインのうち、長い方を総和に加算する」という処理をi=1番のカットラインからi=n-1+m番のカットラインまでおこなっています。この処理をするにあたっては「x番のカットラインの長さ」を求める必要があり、それについては下部のメソッドで計算しています。

メソッドの処理に移ります。まず、カットラインが円の外、すなわち便宜上設定された、刃が素通りするだけのカットラインについては長さが0なので、0を戻します。次に、円の内部にあるカットラインx番の長さを求めていきます。これは、円の中心とカットラインx番の距離をdとしたとき、三平方の定理を用いて2*Math.sqrt(半径^2-d^2)で求まります。

dの計算方法は、まず、n等分した後のそれぞれのパーツの幅が2R/nであることに注目します。また、それぞれのカットラインの長さは、円の中心を軸としたときに線対称になっているので、円の中心よりも下にあるカットラインx番については、n-xと変換することによって、円の中心よりも上にあるカットラインと同じものとして扱うことができます。ここではnが偶数と奇数の場合で場合分けしています。では、この2つの考え方をもとに、距離dを図で表現してみます。

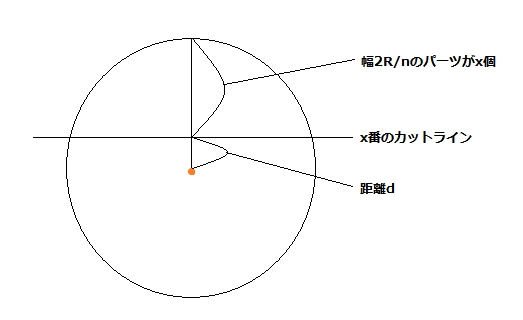
この図を数式で表したものが「d = r - (2*r/n)*x」になります。これでdが求まったので、カットラインx番の長さも求まります。あとは、前述したforループの処理をおこなって終了です。